Nonlinear optical spectroscopy of single
excitonic states
Key words: ultrafast
spectroscopy,
semiconductor nanostructures, excitons, quantum computing, coherent
control, four-wave mixing, heterodyne spectral interferometry, photon
echo, Rabi oscillation
Motivation - Quantum computing
Quantum
computers [1, 2] will be able to perform
calculations that classical computers will never be able to do. The
basic
elements of quantum computer are Qbits that, as ordinary bits,
have two
states. However, in contrast to ordinary bits, qbits can
exist in
quantum superposition of two states. The state of a Qbit can be
conveniently
represented as a Bloch vector on the Bloch sphere (see Fig. 1). In
order to
operate classical bits one needs to switch between 0 and 1 state on
demand. On
the other hand, quantum computing requires the ability to drive the
qbits from
any state to any other in controlled manner. Furthermore, in order to
perform
more advanced operations one must be able to couple different qbits.
Basic
quantum computation operations have now been demonstrated for variety
of
systems [2]. In particular, solid state qbits can be realized by
using localized
excitons in semiconductor nanostructures..
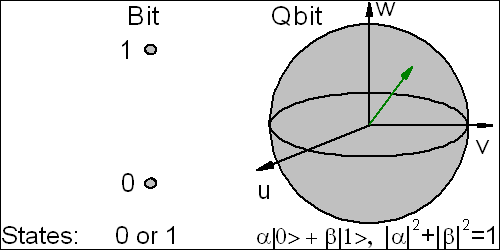
Figure 1
- The bit is an unit of classical information. It can be only in two
discrete states. The Qbit is an unit of quantum information. It can
exist in
a superposition of two states. Qbits are usually represented as
a vector on the Bloch sphere.
Quantum dots and localized excitons
Excitons in semiconductors are
electron-hole pairs bound
by Coulomb attraction. By band gap engineering they can
be
spatially localized. For instance, quantum well excitons are
confined in
the growth direction and move freely in plane of the structure. Yet,
they can
be trapped also in the plane of the quantum well, owing to the
interface fluctuations [8]. As a result, a three-dimensional trapping
potential is
created. Spatially localized excitons can be naturally found in
quantum
dots. In these devices, a region of one material is surrounded by the
other
one, characterized by the larger bandgap. In this project both types of
localized excitons are investigated.
Experimental technique
The influence
of light pulses on the dynamics of localized
excitons (treated as two-level system) is described by optical Bloch
equations.
In particular, the dynamics of the induced polarization in the ensemble
is
governed
by the amplitude decay of the individual polarizations and the mutual
phase
coherence in the ensemble average. However, due to the presence of
inhomognous
broadening, the dephasing of individual transitions is difficult to be
measured. Specifically, the third-order nonlinearity probed in
four-wave mixing
(FWM) can be used to determine homogeneous line-shapes of
inhomogeneously
broadened transitions. Since the size of localized excitonic states in
semiconductors is typically much smaller than the wavelength of the
resonant
light, the light emitted by the polarization of an individual state
propagates
in all directions, so that the commonly used directional selection of
the
four-wave mixing signal is not effective. In order to overcome
this
problem, a novel spectroscopic technique called heterodyne spectral
interferometry has been developed [3, 4]. Conceptually it represents a
combination of the previously used phase-stabilized two-dimensional
femtosecond
spectroscopy and phase-sensitive selection of the non-linear signal
used in
heterodyne-detected four-wave mixing or in phase-cycling detection. The
scheme
of the used experimental setup is presented in Fig. 2.
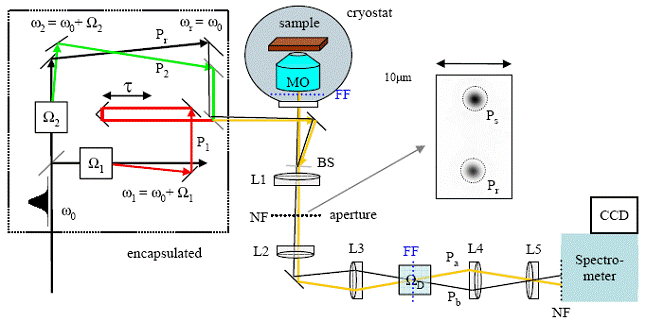
Figure 2 - Scheme of
the experimental setup.
Boxes: Acousto-optical modulators of the indicated frequency. MO: High
numerical aperture (0.85) microscope objective, L1-L5 achromatic
doublet lenses. Spectrometer: Imaging spectrometer of
15 µeV resolution. NF: near field of sample, FF: far-field of
sample.
Recent
advances
Setup and assessment of the technique of
heterodyne-detected single quantum dot transient four-wave mixing
(SQDFWM) [3]
Coherent control and polarization readout of individual excitonic
states [5]
The related experiments were performed on excitons confined by
interface
fluctuations in an AlAs/GaAs/AlAs quantum well (QW) with a nominal GaAs
thickness of 5 nm. Figure 3 (left bottom) shows a FWM spectrum from a
small sample region which is
dominated by a single localized exciton state. Coherent manipulation of
the state vector is presented in figure 3 (right, top) . One can
observe
oscillations of the measured FWM intensity as a function of the pump
pulse area, which due to Rabi oscillations of the state vector.
The damping of the oscillations orginates from the transfer of the
polarization towards near-resonant multiexcitonic states. Coherent
control by the probe pulse on the excitonic transition is
presented in figure 3 (right, bottom). This result demonstrate the
possiblity of
placing state vector for the excitonic transition in any position of
the Bloch sphere. The control of the polarization in amplitude and
phase by detuning of the excitation pulse with respect to the
transition frequency has been demonstrated as well [5].
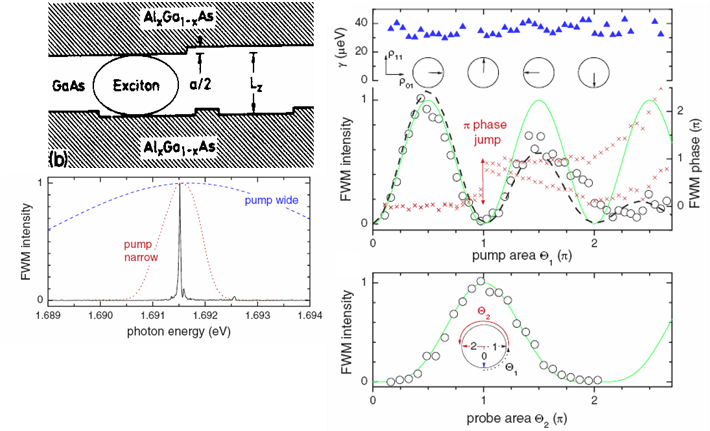
Figure 3 - Coherent control and polarization readout of individual
excitonic states
Photon echo formation in groups
of
individual excitonic
transitions [4, 6]
For positive delay times the FWM signal shows photon echo. Due to the
specific non-linearity probed at this frequency of the FWM, the FWM
phase at a time "tau" after the arrival of the second pulse does not
depend on the eigenfrequency of the two-level system, and thus a
macroscopic polarization is created even in presence of an ensemble of
transitions with different transition energies (inhomogeneous
broadening). This mechanism is illustrated in the left part of Fig. 4.
In a representative measurement, shown in the right part of this figure
the formation of the echo in a finite ensemble is observed as intensity
enhancement at the time of the echo. At this time the FWM fields from
all two-level systems are in phase, and therefore interfere
constructively. This results in a signal amplitude N times larger than
individual FWM amplitude of a single transition. In the limit of a
large number of systems in the ensemble, the signal at t = "tau" is
thus
far larger than at other times, and is called a photon echo. The
formation of the photon echo with increasing number of excitonic
transitions is presented in Fig. 5. Photon echos originating from a
single transition was also measured with heterodyne-spectral
interferometry technique [4, 7]. This is possible due to spectral
wandering of the individual transition.
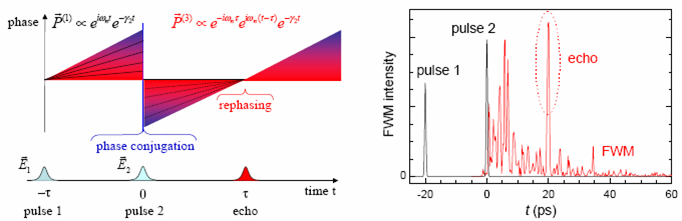
Figure 4 - Left: Scheme of the echo formation in transient FWM. Right:
Measured time-resolved FWM intensity from a group of localized exciton
states. Excitation pulses 1,2 (black) and time-resolved FWM intensity
(red line) for a delay time of "tau" = 20 ps are shown.
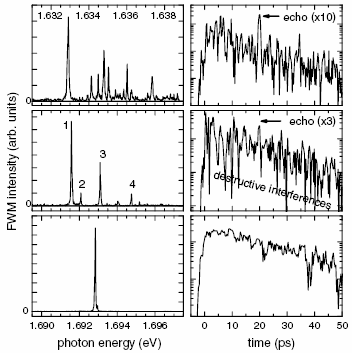
Figure 5 - Measured FWM intensity spectrally- (left-) and time-resolved
(right side) for exciton state ensambles of different size.
Multidimensional spectroscopy in the optical frequency range
[3, 4, 7]
In Fig. 6 we present delay-time
dependent FWM spectra
for a localized exciton system. The strong intensity modulation versus
delay time of some peaks indicate the presence of a coherent coupling
between them. Since we measure the signal in amplitude and phase for
each
delay time tau, we can not only look at the intensity
beating, which is non-straightforward to interpret, but we can also
Fourier-transform the
delay-time dependence of the signal for tau > 0. The result of such
a operation is presented in Fig. 6b. The presence of the
off-diagonal peaks demonstrates the coherent coupling between different
localized excitons.
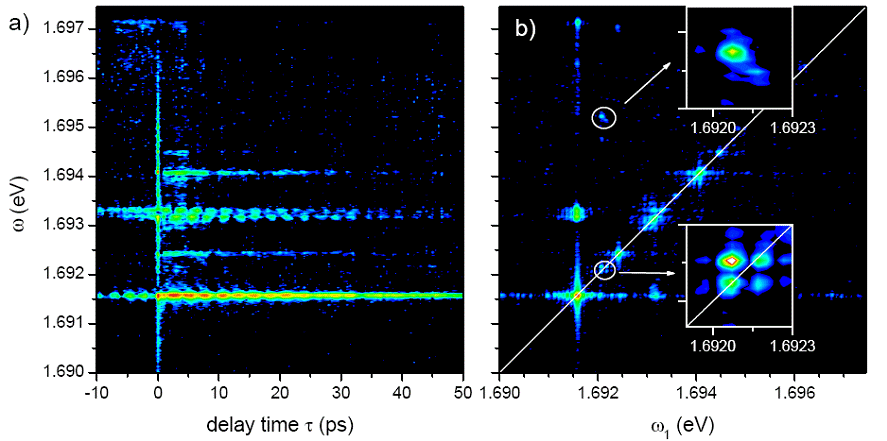
Figure 6 - Two
dimensional FWM measured with heterodyne spectral interferometry
technique.
Present developments
- Demonstration of the coherent coupling between spatially
separated localized excitons.
- Development of a high-resolution optical pulse shaper creating
from an incoming laser pulse four seperate optical pulses, which are
independently shaped in amplitude and phase on a femtosecond to
picosecond time scale.
- Use of coherent optical control of the excitonic states by the
shaped optical pulses to demonstrate simple quantum computational
operations
on coupled exciton states.
References:
- Charles et al. Nature 404,
247 (2000)
- http://en.wikipedia.org/wiki/Quantum_computer,
http://www.cs.caltech.edu/~westside/quantum-intro.html#power,
http://www.quantiki.org/wiki/index.php/Main_Page
- W. Langbein and B. Patton, Optics
Letters 31, 1151, (2006)
- W. Langbein and B. Patton, J. Phys.: Condens. Matter, in press
(2007)
- B. Patton et al., Phys. Rev. Lett.
95,
266401 (2005)
- W. Langbein and B. Patton, Phys. Rev. Lett. 95, 017403 (2005)
- B. Patton et al., Phys. Rev. B 73,
235354 (2006)
- V. Savona and W. Langbein, Phys. Rev. B 74, 075311 (2006)
Project Members
- Wolfgang Langbein (PHYSX)
- Brian Patton (at Oxford University since January 2007)
- Jacek Kasprzak (PHYSX) (since February 2007)

Created by J.Kasprzak and
W.Langbein, 03/2007




