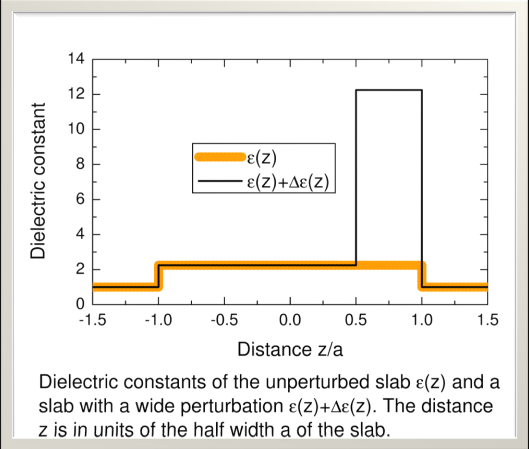
Download Sample Configuration 1 (Slab)
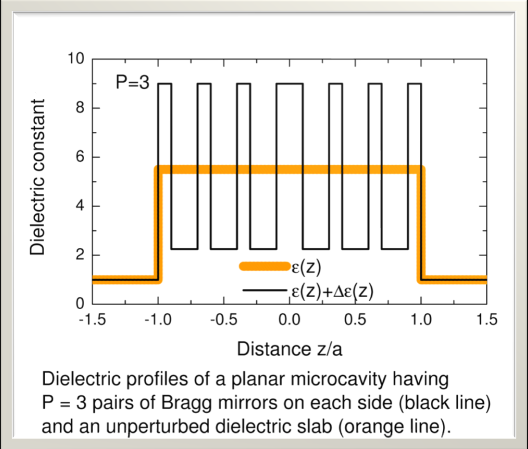
Download Sample Configuration 2 (Bragg mirror cavity)
This page provides and implementation of the Resonant State
Expansion applied to planar open optical systems [2], which is based on the origibnal
application [1]. Recently, we have
applied the theory also to two-dimenesional systems [3], like optical fibres
We provide here an executable program RSE.exe (for microsoft windows 32 bit) implementing the RSE for one-dimensional (planar) systems. Two sample configurations are available, a slab and a Bragg Microcavity.
 Download Sample Configuration 1 (Slab) |
 Download Sample Configuration 2 (Bragg mirror cavity) |
The external boundaries of the perturbed and unperturbed slab are chosen to coincide. The perturbed and unperturbed slabs are surrounded by vacuum. In our sample configurations, the calculation is started from the command line using "RSE.exe Pslab.txt Parameters.txt"
RSE.exe produces two output files:| Re(a*Chi) |
Im(a*Chi) |
M |
AR(1) |
alpha |
a*error |
F |
AR(2) |
| 6.102122e-17 |
-2.344420e-01 |
2.293706e-07 |
1 |
-4.981052e-01 |
3.458102e-08 |
2.548814e+00 |
0 |
| .... |
| Re(a*Chi) |
Extrapolated or perturbed Real part of the perturbed wave number* and multiplied by the unperturbed slab half width |
| Im(a*Chi) |
Extrapolated or perturbed Imaginary part of the perturbed wave number* and multiplied by the unperturbed slab half width |
| M |
Absolute error M given by (21) in our paper |
| AR(1) |
True=1, False=0 that state has been accepted by selection criteria (SC) 2 of our paper |
| alpha |
Power law exponent for the given state as defined by (11) of our paper |
| a*error |
Absolute value of the extrapolation of our perturbed wave number to the exact perturbed wave number estimated using the convergence and extrapolation algorithm as defined in (17) and multiplied by the unperturbed slab half width |
| F |
Relative extrapolation error as defined by (18) in our paper |
| AR(2) |
True=1, False=0 that state has been accept by SC 1 of our paper |
[1] Brillouin-Wigner perturbation theory in open electromagnetic
systems, E. A. Muljarov, W. Langbein and R. Zimmermann, Eurphys.
Lett. 92,50010 (2010) DOI: 10.1209/0295-5075/92/50010
[2] Resonant-state expansion applied to planar open optical
systems M. B. Doost, W. Langbein, and E. A. Muljarov, Phys. Rev. A
85, 023835 (2012) DOI: 10.1103/PhysRevA.85.023835
[3] Resonant state expansion applied to two-dimensional open optical systems M. B. Doost, W. Langbein, and E. A. Muljarov, submitted to Phys. Rev. A (2013), arXiv:1302.0245v1 [physics.optics] 1 Feb 2013